エドワーズ曲線デジタル署名アルゴリズム

エドワーズ曲線デジタル署名アルゴリズム（エドワーズきょくせんデジタルしょめいあるごりずむ、英語: Edwards-curve Digital Signature Algorithm、略称：EdDSA）は、公開鍵暗号において、ツイステッドエドワーズ曲線に基づくシュノア署名の一種を用いたデジタル署名の一つである。他のデジタル署名において見つかっている安全性に関する問題を回避した上で、高効率で暗号化処理が行われるように設計されている。エドワーズ曲線電子署名アルゴリズムは、ダニエル・バーンスタインが率いるチームによって開発された 。

概要

EdDSAのアルゴリズムは以下のように表すことができる。簡単のため、整数や曲線上の点をどのようにビット列に符号化するかといった詳細は省略している。詳細については、引用文献やRFCを参照のこと。

EdDSA方式は、次のパラメータを用いる。

• ${\displaystyle \mathbb {F} _{q}}$：奇素数のべきである ${\displaystyle q}$ を位数として持つ有限体。
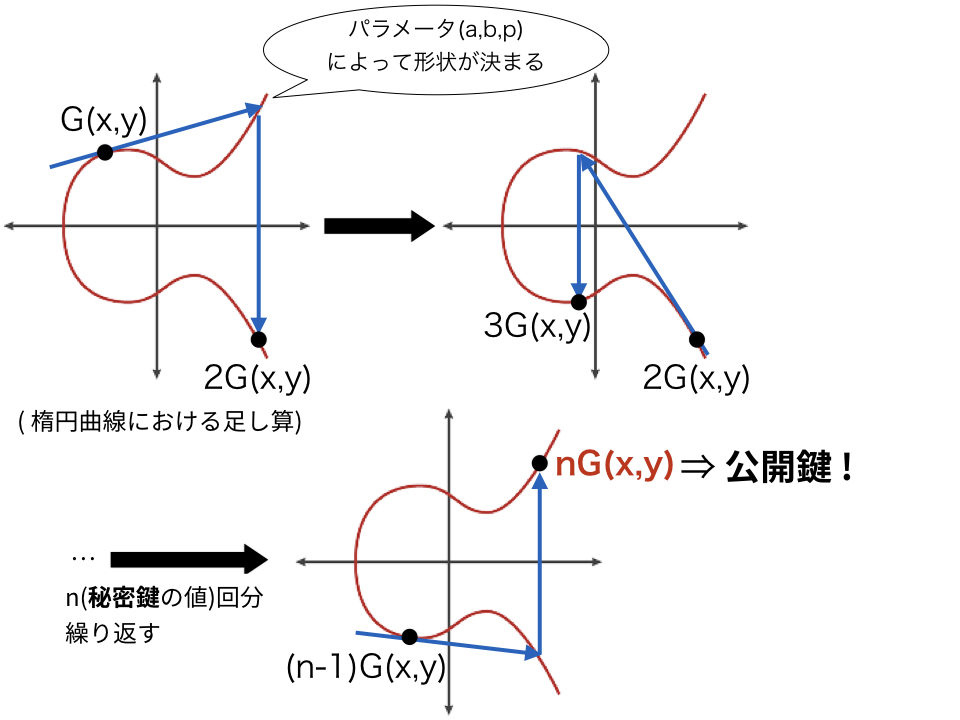
• ${\displaystyle E(\mathbb {F} _{q})}$：${\displaystyle \mathbb {F} _{q}}$ 上の楕円曲線． ただし、位数は大きな素数 ${\displaystyle \ell }$ と適当な自然数 ${\displaystyle c}$ によって ${\displaystyle \#E(\mathbb {F} _{q})=2^{c}\ell }$ で表せる必要がある。${\displaystyle 2^{c}}$ は cofactor と呼ばれる。
• ${\displaystyle B\in E(\mathbb {F} _{q})}$：ベースポイント。位数が ${\displaystyle \ell }$ である楕円曲線上の点。
• ${\displaystyle H}$：出力が ${\displaystyle 2b}$ ビットであるハッシュ関数。ただし、${\displaystyle b}$ は ${\displaystyle 2^{b-1}>q}$ を満たす整数。したがって、${\displaystyle \mathbb {F} _{q}}$ と楕円曲線 ${\displaystyle E(\mathbb {F} _{q})}$ 上の点は、${\displaystyle b}$ ビットで表すことができる。

これらのパラメータは、EdDSA署名方式の全てのユーザが共通で使うことができる。ベースポイントの選択は任意だが、その他のパラメータの選択はEdDSA署名方式の安全性に大きく影響を与える。例えば、ポラード・ロー離散対数アルゴリズムを用いて離散対数を計算するのに必要な楕円加算回数はおよそ ${\displaystyle {\sqrt {\ell \pi /4}}}$ 回である。したがって、このアルゴリズムで離散対数を解くことが事実上できないように ${\displaystyle \ell }$ は十分大きくなければならない。典型的には、${\displaystyle \ell }$ は ${\displaystyle 2^{200}}$ より大きい値を用いる。${\displaystyle \ell }$ の選択は ${\displaystyle q}$ の選択によって制限を受ける。Hasseの定理により、位数${\displaystyle \#E(\mathbb {F} _{q})=2^{c}\ell }$ は、${\displaystyle q 1}$ から ${\displaystyle 2{\sqrt {q}}}$ 以上離れることができないためである。ハッシュ関数 ${\displaystyle H}$ は、EdDSAの安全性解析においては通常ランダムオラクルと想定される。HashEdDSAという変種（variant）においては、${\displaystyle H}$ に加え、衝突耐性を持つハッシュ関数${\displaystyle H'}$も必要である。

鍵生成、署名生成、署名検証の方法は以下の通りである。${\displaystyle \parallel }$ はビット列の連結を表す。

署名鍵

一様ランダムに選んだ ${\displaystyle b}$ ビット列 ${\displaystyle k}$。

公開鍵

署名鍵 ${\displaystyle k}$ から ${\displaystyle s=H_{0,\dots ,b-1}(k)}$ （ハッシュ値の下位 ${\displaystyle b}$ ビット）を計算し、楕円曲線上の点 ${\displaystyle A=sB\in E(\mathbb {F} _{q})}$ を公開鍵とする。${\displaystyle b}$ ビット列で表される。

署名

メッセージ ${\displaystyle M}$ に対する署名は、楕円曲線上の点 ${\displaystyle R}$ と ${\displaystyle \ell }$ 未満の正整数 ${\displaystyle S}$ のペア ${\displaystyle (R,S)}$ で表される。（共に ${\displaystyle b}$ ビットで表せるため、署名長は ${\displaystyle 2b}$ ビット。）これを得るためには、まず署名鍵 ${\displaystyle k}$ から ${\displaystyle k'=H_{b,\dots ,2b-1}(k)}$（ハッシュ値の上位 ${\displaystyle b}$ ビット）を計算し、${\displaystyle r=H(k'\parallel M)}$ を計算する。これを用いて以下を計算する。

$${\displaystyle R=rB}$$$${\displaystyle S=r H(R\parallel A\parallel M)s{\bmod {\ell }}}$$

署名の検証

次の式が成り立つことを確認する。

$${\displaystyle 2^{c}SB=2^{c}R 2^{c}H(R\parallel A\parallel M)A}$$

署名の生成方法と、位数が ${\displaystyle \ell 2^{c}}$ であることから、正しく作られた署名は必ず検証を通る。すなわち： $${\displaystyle {\begin{aligned}2^{c}SB&=2^{c}(r H(R\parallel A\parallel M)s)B\\&=2^{c}rB 2^{c}H(R\parallel A\parallel M)sB\\&=2^{c}R 2^{c}H(R\parallel A\parallel M)A.\end{aligned}}}$$

Ed25519

Ed25519は、エドワーズ曲線デジタル署名の実装の一つであり、ハッシュ関数としてSHA-512（SHA-2）を使い、曲線としてCurve25519を用いている。各パラメータは以下の通り。

• ${\displaystyle q=2^{255}-19}$
• ${\displaystyle E(\mathbb {F} _{q})}$ はツイステッドエドワーズ曲線

$${\displaystyle -x^{2} y^{2}=1-{\frac {121665}{121666}}x^{2}y^{2},}$$

• ${\displaystyle \ell =2^{252} 27742317777372353535851937790883648493}$ および ${\displaystyle c=3}$
• ${\displaystyle B}$ は ${\displaystyle E(\mathbb {F} _{q})}$ 上の点のうち、${\displaystyle y}$ 座標が ${\displaystyle 4/5}$ であり ${\displaystyle x}$ 座標が正である点。
  ただし、"正"とは、点を符号化したビット列について次のように定義される：
  • "正"：座標が偶数（最下位ビットが0）
  • "負"：座標が奇数（最下位ビットが1）
• ${\displaystyle H}$ は SHA-512。したがって ${\displaystyle b=256}$ である。

曲線 ${\displaystyle E(\mathbb {F} _{q})}$ は、Curve25519として知られているモンゴメリ型楕円曲線と双有理同値である。具体的な同値は$${\displaystyle x={\sqrt {-486664}}u/v,\quad y=(u-1)/(u 1)}$$ で与えられる 。

性能

Ed25519は、x86-64 Nehalem/Westmereプロセッサファミリー向けに最適化されている。検証は、64個の署名を一括で処理することでよりスループットを向上させることができる。Ed25519 は、128ビット安全性を持つ共通鍵暗号系と同等の攻撃耐性を提供することを目的としている。公開鍵は256ビット、署名は512ビットである。

コーディングの安全性

安全性に関しては、Ed25519では、秘密のデータに依存した分岐命令と配列参照が用いられておらず、多くのサイドチャネル攻撃に耐性がある。

他の離散対数問題ベースの署名方式と同様に、EdDSAは署名毎に異なるnonceと呼ばれる秘密情報が用いられる。DSAとECDSAにおいては、このnonceは署名生成ごとにランダムに生成されるのが一般的である。しかし、もし脆弱な乱数生成方法が用いられてnonceを推測可能であるときには、署名が秘密鍵の情報を漏らしてしまう。例えば、ソニーのPlayStation 3の署名鍵が漏洩した事例がある。

これに対し、EdDSAでは秘密鍵とメッセージのハッシュ値からnonceを確定的に決めるという方法を取っている。これにより、秘密鍵をランダムに作成すれば、その後の署名生成時には乱数を使う必要がなく、脆弱な乱数生成方法を用いることによる秘密鍵の漏洩のリスクが存在しない。

標準化と実装の矛盾

EdDSAには2つの標準化が存在する。1つはIETFによる RFC 8032 であり、もう1つはNISTによるFIPS 186-5 (2019).である。これらの標準の間の違いについての解析が既に報告されており、テストベクタも利用可能である

ソフトウェア

Ed25519の主要な使用例には、OpenSSH, GnuPGとさまざまな代替ソフトウェア 、そして、OpenBSDで提供されているデジタル署名・署名検証ツールsignifyがある 。

• SUPERCOPのリファレンス実装（インラインアセンブリを含むC言語）
• 速度は遅いが簡潔な別実装。ただし、サイドチャネル攻撃への耐性はない （Python）
• NaCl
• CryptoNote 暗号通貨プロトコル

• wolfSSL
• OpenSSL 1.1.1

Ed448

Ed448は、エドワーズ曲線デジタル署名の実装の一つであり、ハッシュ関数としてSHAKE256を使い、曲線としてCurve448を用いている。Ed25519と同様に、RFC 8032 に定義され、FIPS 186-5の草稿において推奨されている。

脚注

関連項目

• 楕円曲線DSA
• Curve25519
• NaCl (ソフトウェア)

外部リンク

• Ed25519 home page